twelve-tone-equal-temperament.pytwelve-tone-equal-temperament.py
#?##################################################################################################
#?#
#?# Musica - A Music Theory Package for Python
#?# Copyright (C) 2017 Fabrice Salvaire
#?#
#?# This program is free software: you can redistribute it and/or modify
#?# it under the terms of the GNU General Public License as published by
#?# the Free Software Foundation, either version 3 of the License, or
#?# (at your option) any later version.
#?#
#?# This program is distributed in the hope that it will be useful,
#?# but WITHOUT ANY WARRANTY; without even the implied warranty of
#?# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
#?# GNU General Public License for more details.
#?#
#?# You should have received a copy of the GNU General Public License
#?# along with this program. If not, see <http://www.gnu.org/licenses/>.
#?#
#?##################################################################################################
#!# ===============================
#!# Twelve-Tone Equal Temperament
#!# ===============================
#!# This section illustrates the twelve-tone equal temperament (12-TET).
####################################################################################################
import numpy
import matplotlib.pyplot as plt
####################################################################################################
from Musica.Math.MusicTheory import *
from Musica.Theory.Temperament import *
####################################################################################################
fifth_approximations = ET12Tuning.fifth_approximations(number_of_steps_max=20)
print('Perfect fifth 3/2\n 1.5 {:.1f} cent'.format(
float(Cent.from_frequency_ratio(FrequencyRatio.fifth))))
for pitch in fifth_approximations:
print('2**{:2}/{:2} {:.4f} {:.1f} cent'.format(
pitch.number_of_steps,
pitch.step_number,
float(pitch),
float(pitch.cent),
))
#o#
####################################################################################################
number_of_octaves = 10
octave_frequencies = [[ET12.frequency(octave_number, interval_number) for interval_number in range(1, 13)] for octave_number in range(1, number_of_octaves +1)]
all_frequencies = []
for octave_number in range(1, number_of_octaves +1):
frequencies = octave_frequencies[octave_number -1]
all_frequencies += frequencies
print("Octave {:2} {}".format(octave_number, ['{:.2f}'.format(x) for x in frequencies]))
#o#
figure = plt.figure(1, (20, 10))
axe = plt.subplot(111)
axe.set_title('Twelve-tone Equal Temperament')
axe.set_xlabel('notes')
axe.set_ylabel('Hz')
axe.grid()
for octave_number in range(number_of_octaves):
x = octave_number * 12 + 1
axe.axvline(x, color='blue')
axe.text(x, 10, 'Octave {}'.format(octave_number +1), color='black')
axe.semilogy(range(1, len(all_frequencies) +1), all_frequencies, 'o-')
axe.axhline(y=440, color='red')
axe.text(2, 460, 'A 440 Hz', color='black')
axe.axhline(y=50, color='red')
axe.axhline(y=60, color='red')
axe.text(20, 65, 'Electric Network Frequency 50/60Hz', color='black')
axe.axhline(y=20e3, color='red')
axe.text(2, 22e3, 'Human Ear Limit 20 kHz', color='black')
plt.show()
#fig# save_figure(figure, '12tet.png')
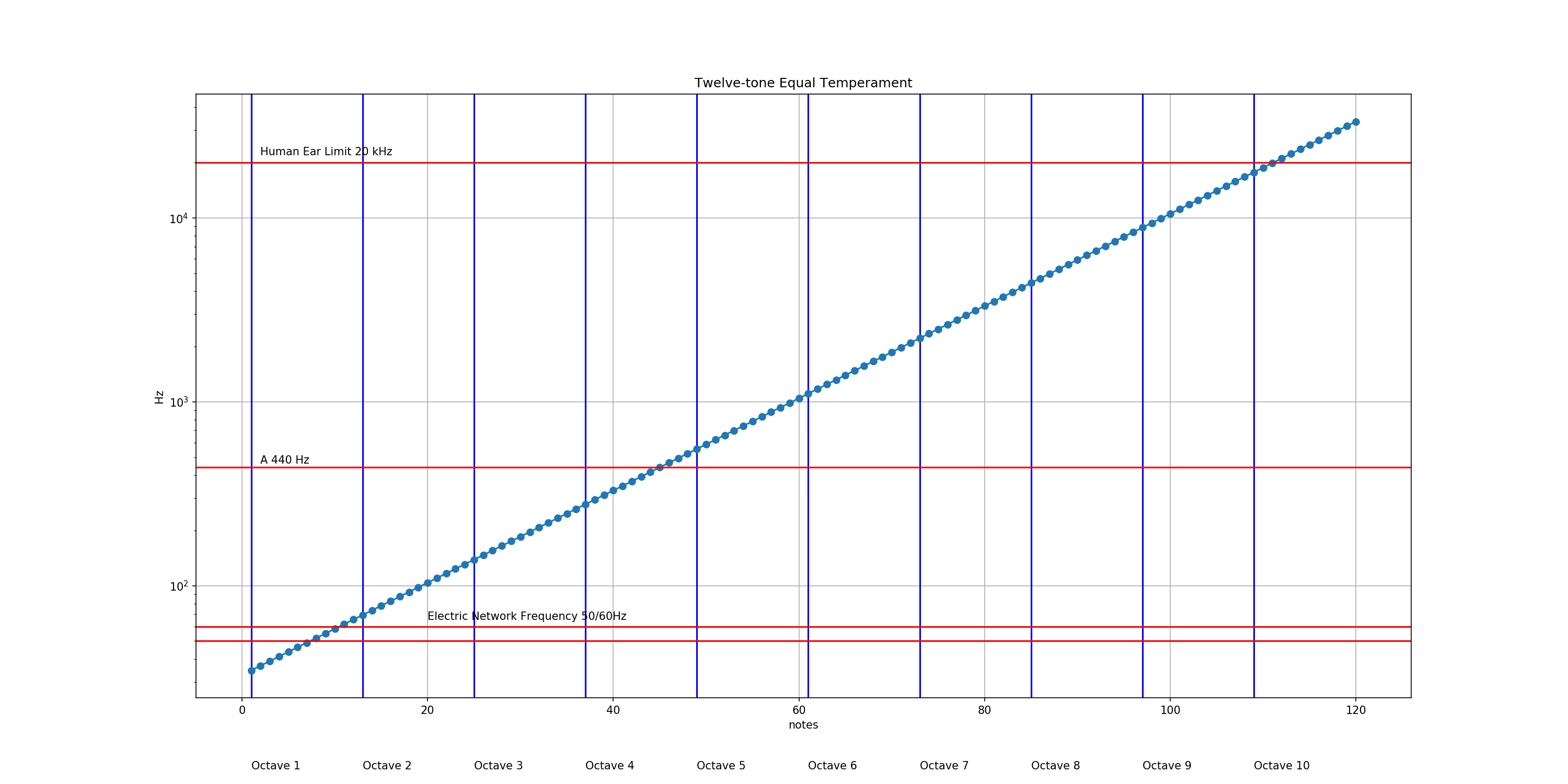
8.3.2. Twelve-Tone Equal Temperament¶
This section illustrates the twelve-tone equal temperament (12-TET).
import numpy
import matplotlib.pyplot as plt
from Musica.Math.MusicTheory import *
from Musica.Theory.Temperament import *
fifth_approximations = ET12Tuning.fifth_approximations(number_of_steps_max=20)
print('Perfect fifth 3/2\n 1.5 {:.1f} cent'.format(
float(Cent.from_frequency_ratio(FrequencyRatio.fifth))))
for pitch in fifth_approximations:
print('2**{:2}/{:2} {:.4f} {:.1f} cent'.format(
pitch.number_of_steps,
pitch.step_number,
float(pitch),
float(pitch.cent),
))
Perfect fifth 3/2
1.5 702.0 cent
2**12/ 7 1.4983 700.0 cent
2**17/10 1.5034 705.9 cent
2**19/11 1.4938 694.7 cent
number_of_octaves = 10
octave_frequencies = [[ET12.frequency(octave_number, interval_number) for interval_number in range(1, 13)] for octave_number in range(1, number_of_octaves +1)]
all_frequencies = []
for octave_number in range(1, number_of_octaves +1):
frequencies = octave_frequencies[octave_number -1]
all_frequencies += frequencies
print("Octave {:2} {}".format(octave_number, ['{:.2f}'.format(x) for x in frequencies]))
Octave 1 ['34.65', '36.71', '38.89', '41.20', '43.65', '46.25', '49.00', '51.91', '55.00', '58.27', '61.74', '65.41']
Octave 2 ['69.30', '73.42', '77.78', '82.41', '87.31', '92.50', '98.00', '103.83', '110.00', '116.54', '123.47', '130.81']
Octave 3 ['138.59', '146.83', '155.56', '164.81', '174.61', '185.00', '196.00', '207.65', '220.00', '233.08', '246.94', '261.63']
Octave 4 ['277.18', '293.66', '311.13', '329.63', '349.23', '369.99', '392.00', '415.30', '440.00', '466.16', '493.88', '523.25']
Octave 5 ['554.37', '587.33', '622.25', '659.26', '698.46', '739.99', '783.99', '830.61', '880.00', '932.33', '987.77', '1046.50']
Octave 6 ['1108.73', '1174.66', '1244.51', '1318.51', '1396.91', '1479.98', '1567.98', '1661.22', '1760.00', '1864.66', '1975.53', '2093.00']
Octave 7 ['2217.46', '2349.32', '2489.02', '2637.02', '2793.83', '2959.96', '3135.96', '3322.44', '3520.00', '3729.31', '3951.07', '4186.01']
Octave 8 ['4434.92', '4698.64', '4978.03', '5274.04', '5587.65', '5919.91', '6271.93', '6644.88', '7040.00', '7458.62', '7902.13', '8372.02']
Octave 9 ['8869.84', '9397.27', '9956.06', '10548.08', '11175.30', '11839.82', '12543.85', '13289.75', '14080.00', '14917.24', '15804.27', '16744.04']
Octave 10 ['17739.69', '18794.55', '19912.13', '21096.16', '22350.61', '23679.64', '25087.71', '26579.50', '28160.00', '29834.48', '31608.53', '33488.07']
figure = plt.figure(1, (20, 10))
axe = plt.subplot(111)
axe.set_title('Twelve-tone Equal Temperament')
axe.set_xlabel('notes')
axe.set_ylabel('Hz')
axe.grid()
for octave_number in range(number_of_octaves):
x = octave_number * 12 + 1
axe.axvline(x, color='blue')
axe.text(x, 10, 'Octave {}'.format(octave_number +1), color='black')
axe.semilogy(range(1, len(all_frequencies) +1), all_frequencies, 'o-')
axe.axhline(y=440, color='red')
axe.text(2, 460, 'A 440 Hz', color='black')
axe.axhline(y=50, color='red')
axe.axhline(y=60, color='red')
axe.text(20, 65, 'Electric Network Frequency 50/60Hz', color='black')
axe.axhline(y=20e3, color='red')
axe.text(2, 22e3, 'Human Ear Limit 20 kHz', color='black')
plt.show()