pythagorean-tuning.pypythagorean-tuning.py
#?##################################################################################################
#?#
#?# Musica - A Music Theory Package for Python
#?# Copyright (C) 2017 Fabrice Salvaire
#?#
#?# This program is free software: you can redistribute it and/or modify
#?# it under the terms of the GNU General Public License as published by
#?# the Free Software Foundation, either version 3 of the License, or
#?# (at your option) any later version.
#?#
#?# This program is distributed in the hope that it will be useful,
#?# but WITHOUT ANY WARRANTY; without even the implied warranty of
#?# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
#?# GNU General Public License for more details.
#?#
#?# You should have received a copy of the GNU General Public License
#?# along with this program. If not, see <http://www.gnu.org/licenses/>.
#?#
#?##################################################################################################
#!# =======================================
#!# Pythagorean Tuning compared to 12-TET
#!# =======================================
#!# This section compares the Pythagorean tuning and the twele-tone equal temperament (12-TET).
####################################################################################################
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
####################################################################################################
from Musica.Math.MusicTheory import *
####################################################################################################
prev_fifth = None
for i, pitch in enumerate(PythagoreanTuning):
delta_numerator = delta_denominator = ''
if isinstance(pitch, PythagoreanFifth):
if prev_fifth is not None:
# 3**7/2**11 apotome |2**8/3**5 limma
delta_numerator, delta_denominator = pitch / prev_fifth
prev_fifth = pitch
print('{:3} {:3} | {:3} {:3} | {:6} / {:6} | {:4.2f} | {:6.0f}'.format(
pitch.numerator_power, pitch.denominator_power,
delta_numerator, delta_denominator,
pitch.numerator, pitch.denominator,
float(pitch), float(pitch.cent)))
#o#
figure1 = plt.figure(1, (20, 10))
axe = plt.subplot(111)
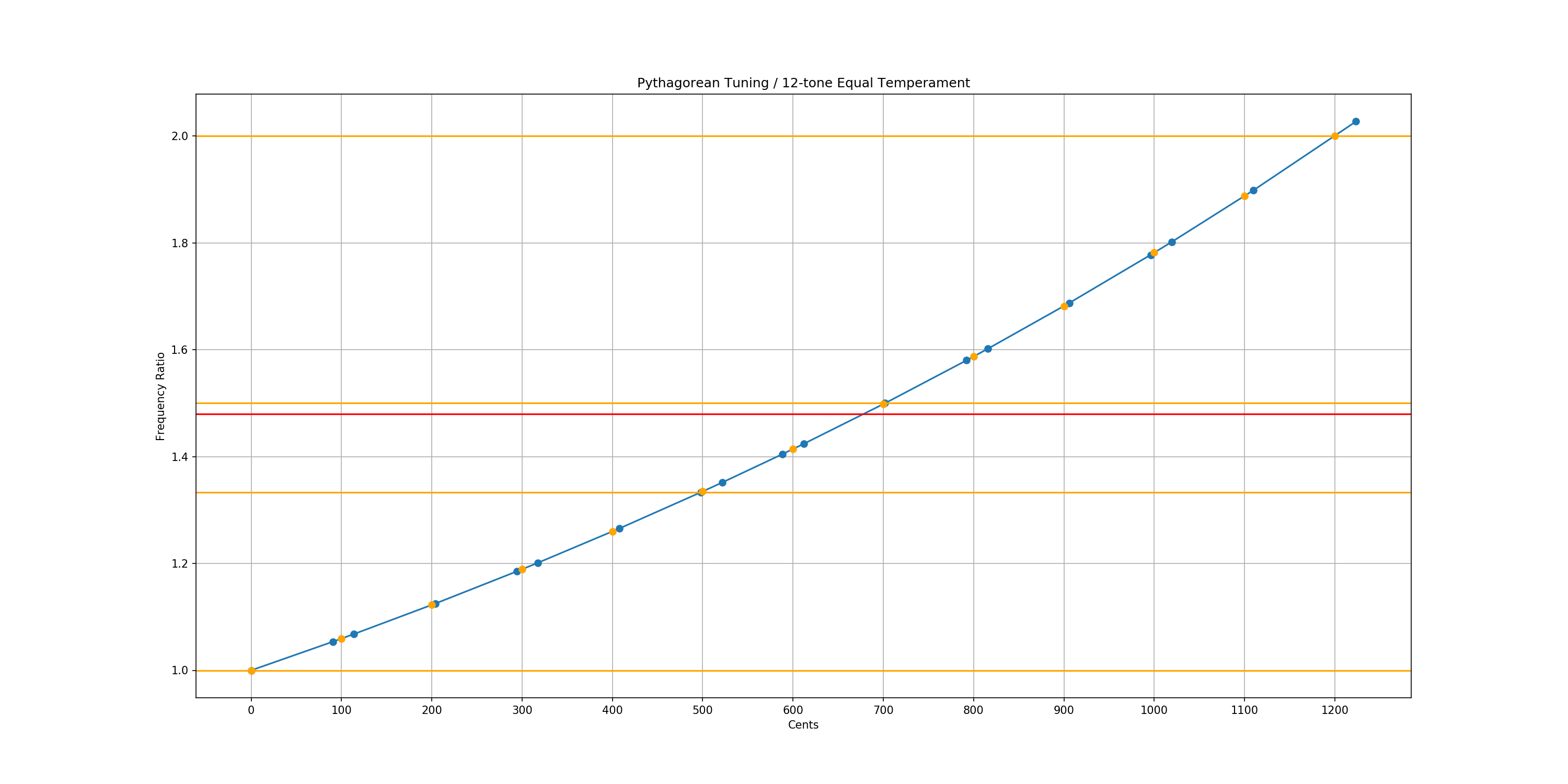
axe.set_title('Pythagorean Tuning / 12-tone Equal Temperament')
axe.set_xlabel('Cents')
axe.set_ylabel('Frequency Ratio')
axe.xaxis.set_major_locator(MultipleLocator(100))
axe.grid()
axe.plot([float(pitch.cent) for pitch in PythagoreanTuning],
[float(pitch) for pitch in PythagoreanTuning],
'o-')
axe.plot([float(pitch.cent) for pitch in ET12Tuning],
[float(pitch) for pitch in ET12Tuning],
'o', color='orange')
for frequency_ratio in (
FrequencyRatio.unisson,
FrequencyRatio.fourth,
FrequencyRatio.fifth,
FrequencyRatio.octave,
):
axe.axhline(y=frequency_ratio, color='orange')
axe.axhline(y=float(PythagoreanTuning.wolf_interval), color='red')
plt.show()
#fig# save_figure(figure1, 'temperament.png')
8.3.1. Pythagorean Tuning compared to 12-TET¶
This section compares the Pythagorean tuning and the twele-tone equal temperament (12-TET).
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
from Musica.Math.MusicTheory import *
prev_fifth = None
for i, pitch in enumerate(PythagoreanTuning):
delta_numerator = delta_denominator = ''
if isinstance(pitch, PythagoreanFifth):
if prev_fifth is not None:
# 3**7/2**11 apotome |2**8/3**5 limma
delta_numerator, delta_denominator = pitch / prev_fifth
prev_fifth = pitch
print('{:3} {:3} | {:3} {:3} | {:6} / {:6} | {:4.2f} | {:6.0f}'.format(
pitch.numerator_power, pitch.denominator_power,
delta_numerator, delta_denominator,
pitch.numerator, pitch.denominator,
float(pitch), float(pitch.cent)))
0 0 | | 1 / 1 | 1.00 | 0
8 5 | | 256 / 243 | 1.05 | 90
7 11 | 11 7 | 2187 / 2048 | 1.07 | 114
2 3 | 8 5 | 9 / 8 | 1.12 | 204
5 3 | | 32 / 27 | 1.19 | 294
9 14 | 11 7 | 19683 / 16384 | 1.20 | 318
4 6 | 8 5 | 81 / 64 | 1.27 | 408
2 1 | | 4 / 3 | 1.33 | 498
11 17 | 11 7 | 177147 / 131072 | 1.35 | 522
10 6 | | 1024 / 729 | 1.40 | 588
6 9 | 8 5 | 729 / 512 | 1.42 | 612
1 1 | 8 5 | 3 / 2 | 1.50 | 702
7 4 | | 128 / 81 | 1.58 | 792
8 12 | 11 7 | 6561 / 4096 | 1.60 | 816
3 4 | 8 5 | 27 / 16 | 1.69 | 906
4 2 | | 16 / 9 | 1.78 | 996
10 15 | 11 7 | 59049 / 32768 | 1.80 | 1020
5 7 | 8 5 | 243 / 128 | 1.90 | 1110
12 18 | 11 7 | 531441 / 262144 | 2.03 | 1223
figure1 = plt.figure(1, (20, 10))
axe = plt.subplot(111)
axe.set_title('Pythagorean Tuning / 12-tone Equal Temperament')
axe.set_xlabel('Cents')
axe.set_ylabel('Frequency Ratio')
axe.xaxis.set_major_locator(MultipleLocator(100))
axe.grid()
axe.plot([float(pitch.cent) for pitch in PythagoreanTuning],
[float(pitch) for pitch in PythagoreanTuning],
'o-')
axe.plot([float(pitch.cent) for pitch in ET12Tuning],
[float(pitch) for pitch in ET12Tuning],
'o', color='orange')
for frequency_ratio in (
FrequencyRatio.unisson,
FrequencyRatio.fourth,
FrequencyRatio.fifth,
FrequencyRatio.octave,
):
axe.axhline(y=frequency_ratio, color='orange')
axe.axhline(y=float(PythagoreanTuning.wolf_interval), color='red')
plt.show()